تبدیل اعداد بین درصد ، کسر (کسر) و اعشار یک مهارت مهم ریاضی است. پس از یادگیری آن خواهید فهمید که مفهوم آن بسیار ساده است. شما نه تنها می دانید چگونه اعداد کوچک را که در امتحانات به شما کمک می کند تبدیل کنید ، بلکه برای انجام محاسبات مالی/مالی نیز مفید خواهد بود.
گام
روش 1 از 3: تغییر درصد

مرحله 1. برای تبدیل درصد به اعشار ، علامت اعشار را دو مکان به سمت چپ حرکت دهید
مگر در موارد دیگری ذکر شده باشد ، در درصد ، نقطه اعشار در انتهای آخرین رقم است. به عنوان مثال ، تصور کنید 75٪ در واقع 75.0٪ به نظر می رسد. حرکت علامت اعشاری دو مکان به چپ ، درصد را به اعشار تبدیل می کند. این روش همان تقسیم یک عدد بر 100 است. مثال:
- 75٪ به 0.75 تغییر کرد
- 3.1 to به 0.031 تغییر کرد
- 0.5 درصد به 0.005 تغییر کرد

مرحله 2. درصد را به صورت کسر 100 نمایش دهید
نوشتن یک عدد به صورت کسر 100 روش ساده دیگری برای نوشتن درصد است. تعداد درصد ، کسر کسر است ، در حالی که 100 مخرج است. کسر را به کوچکترین شکل آن ساده کنید.
- مثال: 36٪ تبدیل به 36/100 می شود.
- برای سادگی ، بالاترین عددی را که در اعداد 36 و 100 قرار دارد پیدا کنید. در این حالت ، عدد 4 است.
- تعیین کنید چند بار 4 به 36 و 100 می رسد. وقتی ساده می کنید ، پاسخ 25/9 است.
- برای بررسی اینکه آیا تبدیل را به درستی انجام داده اید ، 9 را بر 35 (0 ، 36) تقسیم کرده و در 100 (36٪) ضرب کنید. این عدد باید همان درصد اولیه باشد.

مرحله 3. علامت درصد را بردارید
به محض تبدیل درصد به اعشار یا کسر ، استفاده از علامت٪ دیگر مناسب نیست. به خاطر داشته باشید که درصد به معنی "صدم ها" است ، بنابراین اگر فراموش کردید که علامت درصد را پس از تبدیل (به اعشار یا کسر) حذف کنید ، دیگر پاسخ شما به صد مربوط نمی شود.
روش 2 از 3: تبدیل اعشار
مرحله 1. اعشار را در 100 ضرب کنید تا به درصد تبدیل شود
به عبارت دیگر ، نقطه اعشار را دو مکان به راست حرکت دهید. درصد به معنی "صدم" است ، بنابراین اعشار پس از ضرب به "صدم" تبدیل می شود. فراموش نکنید که درصد/علامت (٪) را پس از ضرب اضافه کنید. به عنوان مثال: 0.32 می شود 32، ، 0.07 می شود 7، ، 1.25 می شود 125، ، 0.083 می شود 8.3.

مرحله 2. اعشار انتهایی را به کسر تبدیل کنید
اعشار پایانی یک عدد اعشاری غیرقابل تکرار است. تعداد اعشار را به هر تعداد اعشار به سمت راست حرکت دهید. اکنون عدد ، کسر کسر است. در حالی که مخرج 1 با صفرهای اعشار در عدد اصلی است. به عنوان آخرین مرحله ، کسر را ساده کنید.
- به عنوان مثال: 0 ، 32 دارای دو رقم اعشار است. دو رقم اعشار را به راست حرکت داده و بر 100 تقسیم کنید ، نتیجه این است: 32/100. با 4 به عنوان یک عامل مشترک (عدد و مخرج) ، کسر را می توان به 25/8 تبدیل کرد.
- مثال دیگر: 0 ، 8 فقط یک عدد اعشار دارد. نقطه اعشار را یک مکان به راست حرکت دهید و بر 10 تقسیم کنید ، نتیجه: 8/10. با 2 به عنوان یک عامل مشترک ، کسر را می توان به 4/5 ساده کرد.
- برای بررسی ، می توانید کسر به دست آمده را تقسیم کرده و مطمئن شوید که عدد با اعشار اولیه برابر است: 8/25 = 0.32.

مرحله 3. اعشار تکراری را به کسر تبدیل کنید
اعشار تکراری یک عدد اعشاری است که دارای یک سری اعداد است که به طور مداوم تکرار می شود. به عنوان مثال ، اگر عدد اعشاری تکراری 0 ، 131313 باشد … در آن عدد 2 اعشار تکراری وجود دارد (13 در حال تکرار است). تعیین کنید چه تعداد اعشار اعشاری وجود دارد و سپس اعشار را در 10 ضرب کنید ، جایی که n تعداد اعشار تکراری است.
- به عنوان مثال ، 0 ، 131313 … ضرب در 100 (10 به توان 2) و ما 13 ، 131313 را بدست می آوریم …
- برای تعیین شمارنده (عدد بالا) ، قسمت تکراری را از اعشار کم کنید. به عنوان مثال ، 13 ، 131313… - 0 ، 131313… = 13 ، بنابراین عدد 13 است.
- برای تعیین مخرج (عدد زیر) ، 1 را از عددی که برای ضرب استفاده می کردید ، کم کنید. به عنوان مثال ، 0 ، 131313 … در 100 ضرب می شود ، بنابراین مخرج 100 است - 1 = 99.
- کسر نهایی 0 ، 131313… 13/99 است
-
چند نمونه اضافی:
- 0 ، 333… می شود 3/9
- 0 ، 123123123… می شود 123/999
- 0 ، 142857142857… می شود 142857/999999
- در صورت لزوم ، کسر را به کوچکترین شکل آن تبدیل کنید. به عنوان مثال ، 142857/999999 1/7 می شود.
روش 3 از 3: تبدیل کسرها
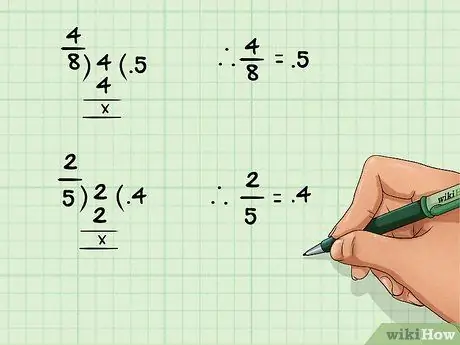
مرحله 1. برای تبدیل کسر به اعشار ، عدد را بر مخرج تقسیم کنید
خط تقسیم بین شمارنده و مخرج را "تقسیم بر" تعریف کنید. به عبارت دیگر ، هر کسری x/y را می توان x تقسیم بر y تفسیر کرد.
به عنوان مثال: کسر 4/8 عدد اعشاری 0.5 را برمی گرداند

مرحله 2. تعداد اعشار را تعیین کنید
بسیاری از اعداد به طور مساوی با یکدیگر تقسیم نمی شوند. اگر آن را تقسیم کنید ، باید تعیین کنید که به چند رقم اعشار نیاز دارید تا پاسخ خود را بدهید. اغلب ، پیش فرض دو رقم اعشار است. هنگام کوتاه کردن کسر ، قانون گرد کردن را به خاطر بسپارید: اگر عدد بعدی 5 است ، عدد قبلی را گرد کنید. به عنوان مثال ، 0.145 به 0.15 گرد می شود.
- به عنوان مثال: کسر 5/17 عدد اعشاری 0 ، 2941176470588 را برمی گرداند…
- آخرین عدد اعشاری را می توان 0.29 نوشت.
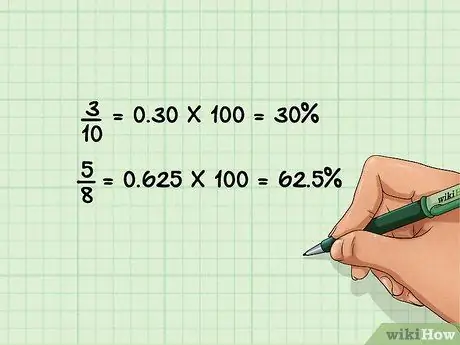
مرحله 3. کسر را تقسیم کرده و سپس در 100 ضرب کنید تا به درصد تبدیل شود
همانطور که کسری را به اعشار تبدیل می کنید ، عدد را بر مخرج تقسیم کنید. عدد اعشاری به دست آمده را در 100 ضرب کرده و نماد درصد (٪) را برای پایان فرآیند تبدیل اضافه کنید.
- اگر 4/8 دارید ، تقسیم 4 بر 8 به شما 0.50 می دهد ، سپس ضرب این عدد در 100 به شما 50 می دهد. افزودن علامت درصد (٪) پاسخ نهایی شما را 50٪ می کند.
-
چند نمونه اضافی:
- 3/10 = 0, 30 * 100 = 30%
- 5/8= 0, 625 * 100 = 62, 5%
نکات
- دانستن جدول زمان بندی کمک زیادی به شما می کند.
- مراقب باشید که معلمان به طور کلی می دانند که آیا کسی از ماشین حساب استفاده کرده است. اگر قرار نیست (طبق قوانین) از ماشین حساب استفاده کنید ، احتمالاً بهتر است این کار را نکنید.
- بسیاری از ماشین حساب ها دارای کلید کسر هستند. ممکن است بتوان از ماشین حساب برای کاهش کسرها به کوچکترین شکل استفاده کرد. برای جزئیات بیشتر ، دفترچه راهنمای ماشین حساب را بخوانید.
هشدار
- مطمئن شوید که نقطه اعشار در جای مناسب قرار دارد.
- هنگام تبدیل از کسر به اعشاری ، حتماً عدد شمارنده را بر مخرج تقسیم کنید.







