تقسیم بر اعداد اعشاری در ابتدا دشوار به نظر می رسد زیرا هیچ کس "0 ، 7 بار جدول" را به شما آموزش نداده است. راز انجام این کار تبدیل مشکل تقسیم به قالبی است که فقط از اعداد کامل استفاده می کند. بعد از اینکه مشکل را به این شکل بازنویسی کردید ، به یک مشکل تقسیم طولانی معمولی تبدیل می شود.
گام
قسمت 1 از 2: مشکلات نوشتاری به عنوان مشکلات تقسیم معمولی
مرحله 1. مشکل تقسیم خود را بنویسید
اگر می خواهید کار خود را بهبود ببخشید ، از مداد استفاده کنید.
-
مثال:
چند تا 3 ÷ 1, 2?

مرحله 2. کل عدد را به صورت اعشاری بنویسید
یک عدد اعشاری بعد از کل عدد بنویسید ، سپس یک صفر بعد از آن اعشار بنویسید. این کار را تا زمانی انجام دهید که هر دو عدد دارای ارزش مکان یکسانی در سمت راست اعشار باشند. این مقدار صحیح را تغییر نمی دهد.
-
مثال:
در مسئله 3 1 ، 2 ، عدد کل ما 3 است. از آنجا که 1 ، 2 دارای ارزش مکانی در سمت راست نقطه اعشار است ، 3 را به صورت 3 ، 0 بنویسید تا این عدد نیز پس از اعشار یک مقدار داشته باشد. حالا ، موضوع ما تبدیل می شود 3, 0 ÷ 1, 2.
- هشدار: صفر را به سمت چپ نقطه اعشار اضافه نکنید! عدد 3 برابر 3 ، 0 یا 3 ، 00 است ، اما برابر 30 یا 300 نیست.

مرحله 3. نقطه اعشار را به راست حرکت دهید تا یک عدد کامل بدست آورید
در مسائل تقسیم ، می توانید اعشاری را منتقل کنید ، اما تنها در صورتی که اعشار اعشاری را بر روی همه اعداد به همان تعداد مراحل حرکت دهید. این به شما امکان می دهد مشکل را به یک عدد کامل تبدیل کنید.
-
مثال:
برای تبدیل 3 ، 0 1 ، 2 به یک عدد کامل ، اعشار را یک مرحله به راست حرکت دهید. بنابراین ، 3 ، 0 می شود 30 و 1 ، 2 می شود 12. اکنون ، مشکل ما می شود 30 ÷ 12.

مرحله 4. مسئله را با استفاده از تقسیم طولانی بنویسید
عدد قابل تقسیم (معمولاً عدد بزرگتر) را در زیر نماد تقسیم بلند قرار دهید. عدد مقسوم را خارج از این نماد بنویسید. در حال حاضر ، شما یک مشکل تقسیم طولانی منظم دارید که از اعداد صحیح استفاده می کند. اگر می خواهید در مورد نحوه انجام تقسیم طولانی یادآوری کنید ، قسمت بعدی را بخوانید.
قسمت 2 از 2: حل مسائل تقسیم طولانی

مرحله 1. اولین رقم پاسخ را بیابید
حل این مسئله را همانطور که معمولاً انجام می دهید ، با مقایسه تقسیم کننده و اولین رقم عدد تقسیم شده شروع کنید. نتیجه تقسیم این رقم اول را بر عدد تقسیم کننده محاسبه کنید ، سپس نتیجه را در بالای آن رقم بنویسید.
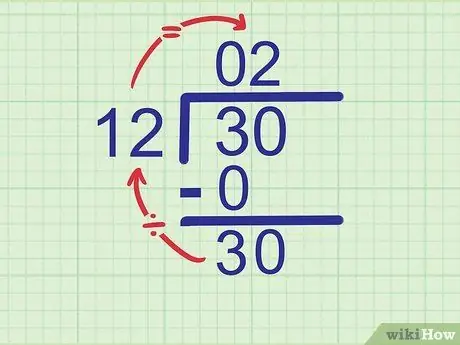
مثال: ما در حال تلاش برای تقسیم 30 بر 12 هستیم. 12 را با اولین رقم عدد تقسیم شده ، یعنی 3 مقایسه کنید. از آنجا که 12 بزرگتر از 3 است ، 3 بر 12 برابر 0 است. بنویسید 0 بالای 3 در خط پاسخ.
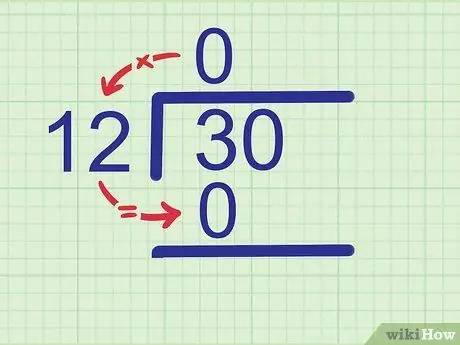
مرحله 2. ضریب را بر تقسیم کننده ضرب کنید
محصول محصول را با عددی که تقسیم شده است بنویسید. نتیجه را دقیقاً زیر اولین رقم عددی که تقسیم کرده اید بنویسید زیرا این رقمی است که به تازگی مشاهده کرده اید.
-
مثال:
از آنجا که 0 12 12 = 0 ، بنویسید 0 زیر 3
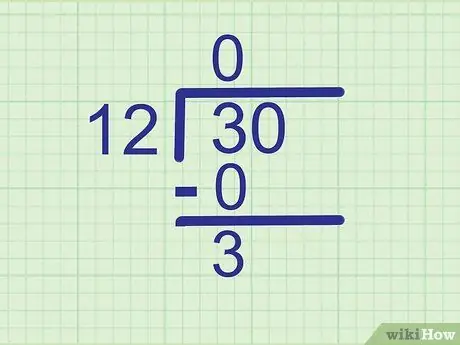
مرحله 3. برای یافتن باقی مانده تفریق کنید
محصولی را که تازه محاسبه کرده اید از رقم مستقیم بالای آن کم کنید. پاسخ را در یک خط جدید ، در زیر آن بنویسید.
-
مثال:
3 - 0 = 3 ، بنابراین بنویسید
مرحله 3 درست زیر 0
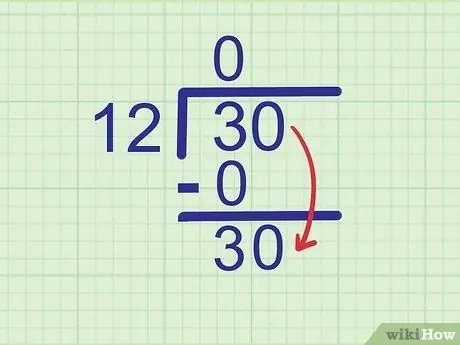
مرحله 4. رقم بعدی را پایین بیاورید
رقم بعدی عدد تقسیم شده را در کنار عددی که تازه یادداشت کرده اید بریزید.
-
مثال:
عددی که تقسیم می شود 30 است. ما عدد 3 را دیده ایم ، بنابراین رقم بعدی که باید پایین بیاید 0 است. عدد 0 را به سمت 3 کاهش دهید تا تبدیل شود
مرحله 30.
مرحله 5. سعی کنید عدد جدید را بر تقسیم کننده تقسیم کنید
اکنون ، اولین مرحله را در این بخش تکرار کنید تا رقم دوم پاسخ خود را بیابید. این بار ، تقسیم کننده را با عددی که در ردیف پایین نوشتید مقایسه کنید.
-
مثال:
ضریب 30 در 12 چقدر است؟ نزدیکترین پاسخی که می توانیم دریافت کنیم 2 است زیرا 12 x 2 = 24. بنویسید
گام 2. در رتبه دوم در خط پاسخ.
- اگر از پاسخ مطمئن نیستید ، چندین ضرب را امتحان کنید تا بزرگترین پاسخ مناسب را پیدا کنید. به عنوان مثال ، اگر برآورد شما 3 است ، 12 3 3 را محاسبه کنید و 36 می گیرید. این عدد بسیار بزرگ است زیرا ما در حال محاسبه 30 هستیم. سعی کنید یک عدد را کاهش دهید ، 12 2 2 = 24. این عدد مناسب است. بنابراین ، 2 پاسخ صحیح است.

مرحله 6. مراحل بالا را برای یافتن شماره بعدی تکرار کنید
این همان فرایند تقسیم طولانی است که در بالا استفاده شد و برای هر مشکل تقسیم طولانی:
- رقم جدید پاسخ خود را بر تقسیم کننده ضرب کنید: 2 * 12 = 24.
- محصول را در یک خط جدید ، زیر عددی که تقسیم شده است بنویسید: 24 را درست زیر 30 بنویسید.
- ردیف پایین را از سطر بالای آن کم کنید: 30 - 24 = 6. بنابراین ، 6 را در یک ردیف جدید در زیر آن بنویسید.

مرحله 7. این روند را ادامه دهید تا آخرین خط پاسخ ها را کامل کنید
اگر هنوز ارقامی در عدد تقسیم شده باقی مانده است ، ارقام را پایین بیاورید و حل مسئله را به همین ترتیب ادامه دهید. اگر آخرین خط پاسخ ها را تکمیل کرده اید ، به مرحله بعدی بروید.
-
مثال:
ما فقط نوشتیم
گام 2. در آخرین خط پاسخ پیش رفتن به مرحله بعدی.

مرحله 8. اعداد اعشاری را برای افزایش "تقسیم" عدد اضافه شده در صورت نیاز اضافه کنید
اگر عدد به طور مساوی قابل تقسیم باشد ، نتیجه تفریق نهایی شما "0" است. این بدان معناست که تقسیم را به پایان رسانده اید و پاسخی را در قالب یک عدد کامل دریافت می کنید. با این حال ، اگر آخرین خط پاسخ ها را تکمیل کرده اید و هنوز ارقامی وجود دارد که می توان آنها را تقسیم کرد ، باید عدد قابل تقسیم را با افزودن یک عدد اعشاری و سپس عدد 0 "گسترش" دهید. در نظر داشته باشید که این مقدار عدد را تغییر ندهید
-
مثال:
ما به آخرین خط پاسخها رسیده ایم ، اما پاسخ آخرین تفریق ما "6" است. با اضافه کردن "، 0" به آخرین رقم ، "6 ، 0" را در زیر نماد تقسیم بلند بنویسید. همچنین نقطه اعشار را در همان محل در خط پاسخ بنویسید ، اما بعد از آن چیزی ننویسید.

مرحله 9. برای پیدا کردن رقم بعدی ، مراحل مشابه را تکرار کنید
تنها تفاوت در اینجا این است که شما باید نقطه اعشار را به همان محل در خط پاسخ اضافه کنید. پس از انجام این کار ، می توانید ارقام پاسخ باقی مانده را دقیقاً به همان شیوه جستجو کنید.
-
مثال:
0 جدید را به آخرین خط بریزید تا "60" شود. از آنجا که 60 تقسیم بر 12 دقیقاً 5 است ، بنویسید
مرحله 5 به عنوان آخرین رقم خط پاسخ ما. فراموش نکنید که ما یک عدد اعشار در خط پاسخ خود قرار می دهیم. بنابراین، 2, 5 آخرین پاسخ به س ourال ما است.
نکات
- می توانید این را به صورت باقیمانده بنویسید (بنابراین پاسخ 3 1 ، 2 "2 باقی مانده 6" است). با این حال ، چون شما با اعشار کار می کنید ، ممکن است معلم شما انتظار داشته باشد که روی قسمت اعشاری پاسخ کار کنید.
- اگر روش تقسیم طولانی را به درستی دنبال کنید ، همیشه یک نقطه اعشار در موقعیت صحیح خواهید داشت ، یا اگر عدد اعشاری بر بخش پذیر قابل تقسیم باشد اصلاً هیچ نقطه اعشار وجود ندارد. سعی نکنید رقم اعشار را حدس بزنید. رقم اعشار اغلب با رقم اعشاری در شماره شروع شما متفاوت است.
- اگر مشکل تقسیم طولانی مدت طولانی طول نکشد ، می توانید متوقف شده و به نزدیکترین عدد گرد کنید. به عنوان مثال ، برای حل 17 4 ، 2 ، فقط تا 4.047 بشمارید … و پاسخ خود را با "حدود 4.05" گرد کنید.
-
شرایط تقسیم بندی خود را به خاطر بسپارید:
- عددی که باید تقسیم شود ، عددی است که باید تقسیم شود.
- مقسوم علیه عددی است که برای تقسیم استفاده می شود.
- ضریب پاسخ مسئله تقسیم ریاضی است.
- کل: تقسیم بر تقسیم کننده = ضریب.
هشدار
به یاد داشته باشید که 30 12 همان پاسخ 3 1 ، 2 را می دهد. سعی نکنید بعد از اینکه اعشار را به عقب حرکت دهید ، پاسخ خود را "تصحیح" کنید
مقالات مرتبط wikiHow
- تبدیل کسرهای رایج به اعشار
- انجام تقسیم بندی طولانی مدت
- کسرها را بر کسرها تقسیم کنید
- تقسیم کسرهای مخلوط







