مقدار P یک اندازه گیری آماری است که به دانشمندان کمک می کند تا فرضیه خود را درست تشخیص دهند. مقدار P برای تعیین اینکه آیا نتایج آزمایش آنها در محدوده مقادیری است که برای موارد مورد مطالعه طبیعی است ، استفاده می شود. معمولاً ، اگر مقدار P یک مجموعه داده از یک مقدار از پیش تعیین شده (به عنوان مثال ، 0.05) پایین بیاید ، دانشمندان فرضیه صفر آزمایش خود را رد می کنند - به عبارت دیگر ، فرضیه ای را که متغیر تجربی دارای آن است رد می کنند. تأثیر قابل توجهی بر نتیجه ندارد. امروزه معمولاً با محاسبه مقدار مجذور کای مقادیر p در جداول مرجع یافت می شود.
گام

مرحله 1. نتایج مورد انتظار آزمایش خود را تعیین کنید
معمولاً ، وقتی دانشمندان آزمایشی را انجام می دهند و نتایج را بررسی می کنند ، از قبل تصوری از نتایج معمولی یا معمولی دارند. این می تواند بر اساس نتایج آزمایش های قبلی ، مجموعه داده های مشاهداتی معتبر ، ادبیات علمی و/یا منابع دیگر باشد. برای آزمایش خود ، نتیجه مورد انتظار خود را تعیین کرده و آن را به صورت عدد بنویسید.
مثال: فرض کنید یک مطالعه قبلی نشان داده بود که در سطح ملی ، بلیط های تندرو بیشتر برای اتومبیل های قرمز صادر می شود تا برای خودروهای آبی. فرض کنید میانگین نتیجه در سطح کشور نسبت 2: 1 را نشان می دهد و نسبت خودروهای قرمز بیشتر است. ما می خواهیم با تجزیه و تحلیل سرعت مجاز صادر شده توسط پلیس در شهرمان ، متوجه شویم که آیا پلیس شهر ما نیز همین گرایش را دارد یا خیر. اگر ما یک نمونه تصادفی از 150 بلیط سرعت مجاز که به خودروهای قرمز و آبی در شهرمان داده شده بود ، بگیریم ، انتظار داریم 100 برای ماشین قرمز و 50 اگر ماشین پلیس در شهر ما طبق مقایسه در سطح ملی بلیط می دهد ، برای اتومبیل های آبی.

مرحله 2. مشاهدات تجربی خود را تعیین کنید
اکنون که مقدار مورد انتظار خود را تعیین کرده اید ، می توانید آزمایش خود را اجرا کرده و مقدار واقعی (یا مشاهده) را بیابید. مجدداً نتیجه را به صورت عدد یادداشت کنید. اگر برخی از شرایط آزمایشی را دستکاری کنیم و نتایج مشاهده شده با نتایج مورد انتظار متفاوت باشد ، دو احتمال وجود دارد: یا این به طور تصادفی اتفاق افتاده است ، یا دستکاری ما بر متغیرهای آزمایشی است که باعث این تفاوت شده است. هدف از یافتن مقدار p اساساً تعیین این است که آیا نتایج مشاهده شده با نتایج مورد انتظار متفاوت است تا جایی که فرضیه صفر-این فرضیه که هیچ رابطه ای بین متغیر آزمایشی و نتایج مشاهده شده وجود ندارد-رد شود.
مثال: فرض کنید ، در شهر ما ، 150 بلیط سرعت مجاز را به طور تصادفی انتخاب می کنیم که به خودروهای قرمز و آبی تعلق می گیرد. ما گرفتیم 90 بلیط ماشین قرمز و 60 برای ماشین آبی این با نتیجه ای که انتظار داشتیم متفاوت است ، یعنی 100 و 50 به آیا دستکاری آزمایشی ما (در این مورد ، تغییر منبع داده از ملی به محلی) تغییری در نتایج ایجاد کرد ، یا پلیس شهر ما گرایش های مشابهی در سطح ملی داشت و ما فقط تصادف را مشاهده کردیم؟ مقدار p به ما در تعیین آن کمک می کند.

مرحله 3. درجه آزادی آزمایش خود را تعیین کنید
درجات آزادی اندازه گیری میزان تنوع در مطالعه است که با توجه به تعداد دسته هایی که بررسی می کنید تعیین می شود. معادله درجات آزادی برابر است درجات آزادی = n-1 ، جایی که n تعداد دسته ها یا متغیرهای تجزیه و تحلیل شده در آزمایش شما است.
-
مثال: آزمایش ما دارای دو دسته نتایج است: یکی برای ماشین قرمز و دیگری برای ماشین آبی. بنابراین ، در آزمایش ما 2-1 = داریم 1 درجه آزادی
اگر اتومبیل های قرمز ، آبی و سبز را مقایسه کنیم ، خواهیم داشت
گام 2. درجات آزادی و غیره

مرحله 4. نتایج مورد انتظار را با نتایج مشاهده شده با استفاده از مجذور کای مقایسه کنید
مربع چی (x نوشته شده است2) یک مقدار عددی است که تفاوت بین مقادیر مورد انتظار و مشاهده شده از آزمایش را اندازه گیری می کند. معادله chi مربع عبارت است از: ایکس2 = ((o-e)2/ه) ، که در آن مقدار مشاهده شده و e مقدار مورد انتظار است. نتایج این معادله را برای همه نتایج احتمالی جمع کنید (به پایین مراجعه کنید).
- توجه داشته باشید که این معادله از عملگر (sigma) استفاده می کند. به عبارت دیگر ، شما باید محاسبه کنید ((| o-e | -05)2/ه) برای هر نتیجه احتمالی ، سپس نتایج را جمع کنید تا مقدار مربع چی را بدست آورید. در مثال ما ، دو نتیجه داریم - خودرویی که بلیط قرمز یا آبی دریافت می کند. بنابراین ، می توانیم محاسبه کنیم ((o-e)2/ه) دو بار - یک بار برای ماشین قرمز و یک بار برای ماشین آبی.
-
مثال: بیایید مقادیر و مشاهدات مورد انتظار خود را به معادله x وصل کنیم2 = ((o-e)2/ه) به یاد داشته باشید که به دلیل عملگر سیگما ، باید محاسبه کنیم ((o-e)2/ه) دو بار - یک بار برای ماشین قرمز و یک بار برای ماشین آبی. مراحل پردازش به شرح زیر است:
- ایکس2 = ((90-100)2/100) + (60-50)2/50)
- ایکس2 = ((-10)2/100) + (10)2/50)
- ایکس2 = (100/100) + (100/50) = 1 + 2 = 3.

مرحله 5. سطح اهمیت را انتخاب کنید
اکنون که ما درجه آزادی کیت آزمایشی و مقدار مربع چی را می دانیم ، تنها یک مورد قبل از یافتن مقدار p ما وجود دارد-ما باید سطح اهمیت را تعیین کنیم. اساساً ، سطح اهمیت اندازه گیری میزان اطمینان ما از نتایج خود است - سطح پایین اهمیت مربوط به احتمال کمی است که نتیجه یک آزمایش به دلیل شانس بوده و بالعکس. سطح اهمیت به صورت اعشاری نوشته می شود (به عنوان مثال 01/0) ، که با درصد احتمال اینکه نتیجه آزمایش ناشی از شانس بوده (در این مورد ، 1 s) مطابقت دارد.
- طبق توافق ، دانشمندان معمولاً برای آزمایشات خود مقدار معنی داری را 0.05 یا 5 درصد تعیین می کنند. این بدان معناست که نتایج تجربی که با این سطح از اهمیت مطابقت دارد ، حداکثر 5 درصد احتمال تصادف دارند. به عبارت دیگر ، 95 chance احتمال وجود دارد که نتایج به دلیل دستکاری دانشمند بر متغیرهای آزمایشی باشد ، و نه تصادفی. برای اکثر آزمایشات ، 95٪ اطمینان در مورد رابطه بین دو متغیر ، در نشان دادن رابطه بین این دو موفق بوده است.
- مثال: برای مثال ماشین قرمز و آبی ما ، اجازه دهید توافق علمی را دنبال کرده و سطح اهمیت خود را تعیین کنیم 0, 05.
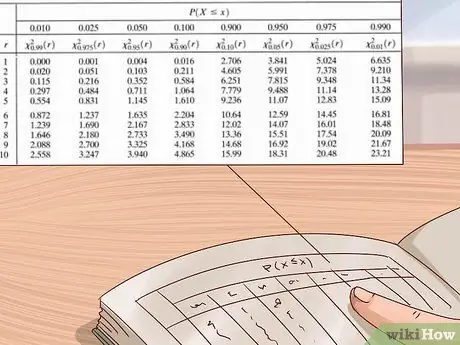
مرحله 6. برای برآورد مقدار p خود از جدول توزیع مربع کای استفاده کنید
دانشمندان و آمارشناسان از جداول بزرگ مقادیر برای محاسبه مقادیر p برای آزمایشات خود استفاده می کنند. این جدول معمولاً با محور عمودی در سمت چپ که درجات آزادی را نشان می دهد و محور افقی در بالا مقادیر p را نشان می دهد. با استفاده از این جدول ابتدا درجه آزادی خود را بیابید ، سپس سطرها را از چپ به راست بخوانید تا اولین مقداری که بیشتر از مقدار مربع چی شما است را بیابید. به مقدار p در بالای ستون نگاه کنید-مقدار p شما بین این مقدار و بزرگترین مقدار بعدی است (مقدار سمت راست در سمت چپ آن قرار دارد).
- جداول توزیع Chi square از منابع مختلف در دسترس هستند - می توان آنها را به راحتی در اینترنت یا در کتاب های علوم یا آمار یافت. اگر یکی ندارید ، از جدول نشان داده شده در عکس بالا یا یک جدول آنلاین رایگان ، مانند جدولی که medcalc.org در اینجا ارائه کرده است ، استفاده کنید.
-
مثال: مربع چی ما 3 است. بنابراین بیایید از جدول توزیع مربع چی در عکس بالا برای پیدا کردن مقدار p تقریبی استفاده کنیم. از آنجا که ما می دانیم که آزمایش ما فقط دارد
مرحله 1 درجه آزادی ، ما از جدول بالا شروع می کنیم. در این ردیف از چپ به راست می رویم تا مقداری بالاتر از آن پیدا کنیم
مرحله 3 - مقدار مربع چی ما اولین مقداری که پیدا می کنیم 3.84 است. با جستجوی این ستون می بینیم که مقدار p مربوطه 0.05 است. این بدان معناست که مقدار p ما بین 0.05 تا 0.1 (بزرگترین p-value بعدی در جدول).

مرحله 7. تصمیم بگیرید که آیا فرضیه صفر خود را رد یا دفاع کنید
از آنجا که مقدار p تقریبی برای آزمایش خود پیدا کرده اید ، می توانید تصمیم بگیرید که آیا فرضیه صفر آزمایش خود را رد کنید یا نه (به عنوان یادآوری ، این فرضیه است که متغیر آزمایشی که دستکاری کرده اید هیچ تاثیری بر نتایج مشاهده شده نداشته است). اگر مقدار p شما کمتر از مقدار اهمیت شماست ، تبریک می گوییم-شما ثابت کرده اید که احتمال زیادی وجود دارد که بین متغیرهایی که دستکاری کرده اید و مشاهدات شما رابطه وجود داشته باشد. اگر مقدار p شما بیشتر از مقدار اهمیت شما باشد ، نمی توانید با اطمینان بگویید که نتایجی که مشاهده می کنید نتیجه تصادف یا دستکاری آزمایش شما است.
- مثال: مقدار p ما بین 0.05 تا 0.1 است. یعنی به هیچ وجه کمتر از 0.05 نیست ، بنابراین متأسفانه ما نمی تواند فرضیه صفر ما را رد کند به این بدان معناست که ما به حداقل 95 درصد اطمینان که تعیین کرده ایم نمی رسیم تا بتوان گفت پلیس شهر ما بلیط بلیط را به خودروهای قرمز و آبی نسبت می دهد که با میانگین کشوری کاملاً متفاوت است.
- به عبارت دیگر ، 5 تا 10 chance احتمال وجود دارد که مشاهدات ما نتیجه تغییر مکان (تجزیه و تحلیل شهر ما و نه کل قسمت) نباشد ، بلکه تصادفی باشد. از آنجا که ما به دنبال احتمال کمتر از 5 هستیم ، نمی توانیم بگوییم که ما متقاعد که پلیس شهر ما تمایل دارد خودروهای قرمز را بلیط کند - این احتمال کمی وجود دارد اما از نظر آماری بسیار متفاوت است که آنها این گرایش را ندارند.
نکات
- یک ماشین حساب علمی محاسبات را بسیار ساده تر می کند. همچنین می توانید ماشین حساب ها را به صورت آنلاین جستجو کنید.
- شما می توانید مقادیر p را با استفاده از چندین برنامه کامپیوتری ، از جمله نرم افزارهای صفحه گسترده و نرم افزارهای آماری تخصصی تر محاسبه کنید.







