نحوه محاسبه بزرگنمایی لنز: 12 مرحله (همراه با تصاویر)

2024 نویسنده: Jason Gerald | [email protected]. آخرین اصلاح شده: 2024-01-16 19:24

در مطالعه ابزارهای نوری ، "بزرگنمایی" یک شیء شبیه به عدسی ، نسبت ارتفاع تصویری است که مشاهده می کنید به ارتفاع واقعی جسم. به عنوان مثال ، لنزی که می تواند یک جسم را بسیار بزرگ نشان دهد دارای ضریب بزرگنمایی "زیاد" است ، در حالی که لنزی که یک شی را کوچک نشان می دهد دارای ضریب بزرگنمایی "کم" است. فرمول بزرگنمایی یک شی معمولاً با استفاده از فرمول محاسبه می شود M = (ساعت_من/ساعت_o) = -(د_من/د_o) ، جایی که M = بزرگنمایی ، h_من = ارتفاع تصویر ، ساعت_o = ارتفاع جسم ، و د_من و دی_o = فاصله تصویر و شی

گام

روش 1 از 2: محاسبه بزرگنمایی یک لنز

یادداشت ها: الف عدسی همگرا در مرکز بیشتر از لبه ها (مانند ذره بین). آ عدسی واگرا در لبه ها گسترده تر از مرکز (مانند یک کاسه). محاسبه بزرگنمایی در هر دو لنز یکسان است ، با یک استثناء مهم به برای رفتن مستقیم به استثنائات لنزهای واگرا اینجا را کلیک کنید.

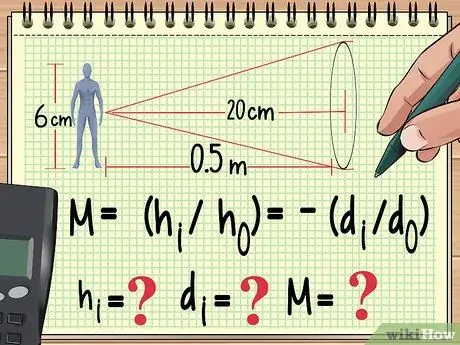
مرحله 1. با معادله خود و متغیرهایی که از قبل می شناسید شروع کنید

درست مانند هر مسئله فیزیک دیگر ، راه حل مسئله بزرگنمایی این است که معادله ای را که برای محاسبه آن استفاده می کنید بنویسید. از اینجا ، می توانید به صورت معکوس کار کنید تا مقدار متغیری را که از معادله ای که استفاده می کنید پیدا نکرده اید ، بیابید.

• به عنوان مثال ، فرض کنید یک عروسک با ارتفاع 6 سانتی متر در یک متری a قرار داده شده است عدسی همگرا با فاصله کانونی 20 سانتی متر اگر می خواهیم بزرگنمایی ، ارتفاع تصویر و فاصله تصویر را محاسبه کنیم ، می توانیم معادله خود را به صورت زیر بنویسیم:

  M = (ساعت_من/ساعت_o) = -(د_من/د_o)

• اکنون می دانیم h_o (ارتفاع عروسک) و د_o (فاصله عروسک از لنز). ما همچنین فاصله کانونی عدسی را می دانیم که در این معادله نیست. خواهیم شمرد ساعت_من، د_من، و م.

مرحله 2. استفاده از معادله عدسی برای بدست آوردن d_من.

اگر فاصله از جسم موردنظر خود را بزرگ کرده و فاصله کانونی عدسی را بدانید ، محاسبه فاصله از تصویر تشکیل شده با معادله لنز بسیار آسان است. معادله عدسی است 1/f = 1/d_o + 1/روز_من ، جایی که f = فاصله کانونی عدسی است.

• در این مثال مثال ، می توانیم از معادله عدسی برای محاسبه d استفاده کنیم_منبه مقادیر f و d را وارد کنید_من سپس معادله را حل کنید:

  1/f = 1/d_o + 1/روز_من

  1/20 = 1/50 + 1/روز_من

  5/100 - 2/100 = 1/روز_من

  3/100 = 1/روز_من

  100/3 = د_من = 33.3 سانتی متر

• فاصله کانونی عدسی فاصله مرکز لنز تا نقطه ای است که نور در نقطه کانونی منتقل می شود. اگر تا به حال نور را با ذره بین بر روی سوزاندن مورچه ها متمرکز کرده اید ، آن را دیده اید. در س questionsالات درس ، معمولاً بزرگی این نقطه مهم آورده شده است. در زندگی واقعی ، این مشخصات معمولاً روی برچسبی که روی عدسی قرار دارد نوشته می شود.

مرحله 3. محاسبه h_من.

بعد از محاسبه d_o و دی_من، می توانید ارتفاع جسم بزرگ شده و بزرگنمایی عدسی را محاسبه کنید. در معادله بزرگنمایی عدسی به دو علامت مساوی توجه کنید (M = (h_من/ساعت_o) = -(د_من/د_o)) - این بدان معناست که تمام قسمتهای این معادله برابر یکدیگر هستند ، بنابراین ما می توانیم M و h را محاسبه کنیم_من به هر ترتیبی که بخواهیم

• برای این مثال مثال ، می توانیم h را محاسبه کنیم_من مثل این:

  (ساعت_من/ساعت_o) = -(د_من/د_o)

  (ساعت_من/6) = -(33, 3/50)

  ساعت_من = -(33 ، 3/50) x 6

  ساعت_من = - 3 ، 996 سانتی متر

• توجه داشته باشید که ارتفاع جسم در اینجا منفی است که نشان می دهد تصویری که بعداً خواهیم دید معکوس می شود (بالا-پایین).

مرحله 4. محاسبه M

می توانید آخرین متغیر را با معادله -(د_من/د_o) یا (ساعت_من/ساعت_o).

• در مثال زیر نحوه محاسبه M به شرح زیر است:

  M = (ساعت_من/ساعت_o)

  M = (-3 ، 996/6) = - 0, 666

• هنگام محاسبه مقدار d نیز نتیجه یکسان خواهد بود:

  M = -(د_من/د_o)

  M = -(33 ، 3/50) = - 0, 666

• توجه داشته باشید که زوم برچسب واحد ندارد.

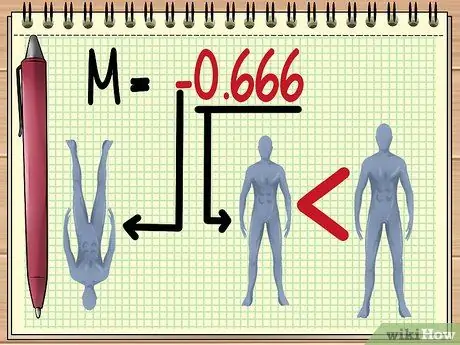
مرحله 5. درک مقدار M

هنگامی که مقدار M را بدست آورید ، می توانید چندین مورد را در مورد تصویری که از لنز مشاهده خواهید کرد برآورد کنید ، یعنی:

• اندازه.

  هرچه "مقدار مطلق" M بیشتر باشد ، جسم مشاهده شده با لنز بزرگتر ظاهر می شود. مقدار M بین 0 تا 1 نشان می دهد که شی کوچکتر به نظر می رسد.

• جهت گیری شی

  مقدار منفی نشان می دهد که تصویر تشکیل شده معکوس می شود.

• در مثال ارائه شده در اینجا ، مقدار M -0.666 به این معنی است که با توجه به مقدار متغیر موجود ، سایه عروسک قابل مشاهده خواهد بود. وارونه و دو سوم کوچکتر از اندازه واقعی.

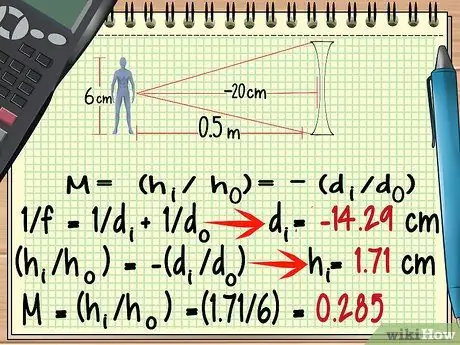
مرحله 6. برای لنزهای واگرا ، از یک نقطه کانونی منفی استفاده کنید

اگرچه شکل یک لنز واگرا بسیار متفاوت از یک لنز همگرا است ، اما می توانید بزرگنمایی آن را با استفاده از فرمول مشابه بالا محاسبه کنید. استثنائاتی که باید در نظر داشته باشید عبارتند از: نقطه کانونی عدسی واگرا منفی است.

در مثال مثال بالا ، این بر پاسخی که در محاسبه d دریافت می کنید تأثیر می گذارد_من، بنابراین مطمئن شوید که به این موضوع توجه کرده اید.

• بیایید مشکل مثال بالا را دوباره کار کنیم ، فقط اکنون از یک لنز واگرا با فاصله کانونی استفاده می کنیم - 20 سانتی متر

  سایر متغیرها همان مقدار باقی می مانند.

• اول از همه ، d را محاسبه می کنیم_من با استفاده از معادله عدسی:

  1/f = 1/d_o + 1/روز_من

  1/-20 = 1/50 + 1/روز_من

  -5/100 - 2/100 = 1/روز_من

  -7/100 = 1/روز_من

  -100/7 = د_من = - 14 ، 29 سانتی متر

• اکنون h را محاسبه می کنیم_من و M با مقدار d_من جدید

  (ساعت_من/ساعت_o) = -(د_من/د_o)

  (ساعت_من/6) = -(-14, 29/50)

  ساعت_من = -(- -14 ، 29/50) x 6

  ساعت_من = 1 ، 71 سانتی متر

  M = (ساعت_من/ساعت_o)

  M = (1 ، 71/6) = 0, 285

روش 2 از 2: محاسبه بزرگنمایی لنزهای چندگانه

روش ساده دو لنز

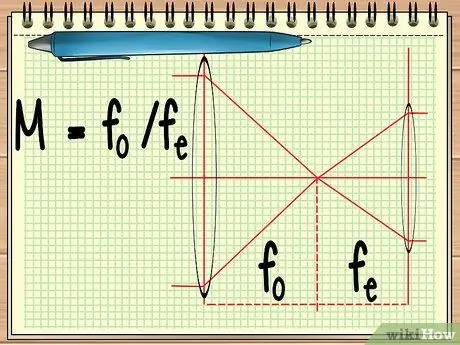
مرحله 1. نقطه کانونی دو عدسی را محاسبه کنید

هنگامی که از ابزاری استفاده می کنید که شامل دو لنز است که در کنار هم قرار گرفته اند (مانند تلسکوپ یا یک دوربین دو چشمی) ، تنها چیزی که باید بدانید نقطه کانونی دو لنز است تا بزرگنمایی کلی دو لنز را محاسبه کنید. این را می توان با معادله ساده M = f محاسبه کرد_o/f_ه.

در معادله ، f_o نقطه کانونی عدسی عینی است و f_ه نقطه کانونی چشمی است. عدسی شیئی لنز بزرگی است که نزدیک به جسم است ، در حالی که عدسی چشمی لنزی است که نزدیک چشم ناظر واقع شده است.

مرحله 2. اطلاعاتی را که از قبل دارید به معادله M = f وصل کنید_o/f_ه.

وقتی نقاط کانونی هر دو لنز را بدست آورید ، محاسبه آنها بسیار آسان است - نسبت را با تقسیم فاصله کانونی لنزهای عینی به فاصله کانونی چشمی محاسبه کنید. پاسخی که می گیرید بزرگنمایی کل ابزار است.

• به عنوان مثال ، فرض کنید یک تلسکوپ ساده نوشته شده است که نقطه کانونی عدسی شیئی 10 سانتی متر و نقطه کانونی چشمی 5 سانتی متر است ، سپس بزرگنمایی 10/5 = 2.

روش پیچیده

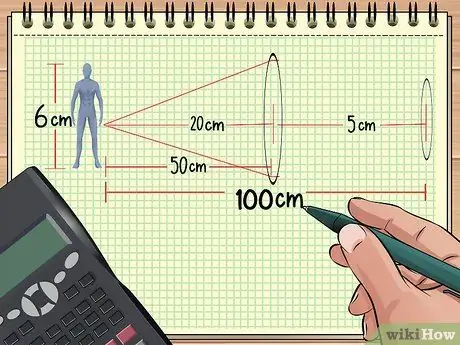
مرحله 1. فاصله بین لنزها و جسم را محاسبه کنید

اگر دو لنز پشت سر هم در یک ردیف مرتب شده باشید ، اگر فاصله لنزها تا جسم ، اندازه جسم و نقطه کانونی دو لنز را بدانید ، بزرگنمایی کل را می توان محاسبه کرد. باقی مانده را نیز می توان محاسبه کرد.

برای مثال ، فرض کنید ما اشیاء و لنزها را مانند مثال شماره 1 بالا مرتب می کنیم: یک عروسک 50 سانتیمتر از یک لنز همگرا که فاصله کانونی 20 سانتی متر دارد فاصله دارد. اکنون ، عدسی دوم را با نقطه کانونی 5 سانتی متر در فاصله 50 سانتی متری از لنز اول (100 سانتی متر از عروسک) قرار دهید. پس از این ، کل بزرگنمایی را با استفاده از اطلاعاتی که به دست آورده ایم محاسبه می کنیم

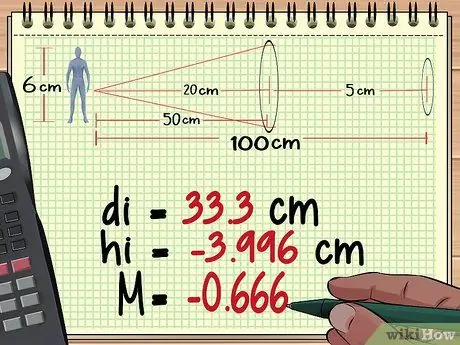
مرحله 2. فاصله ، ارتفاع و بزرگنمایی جسم را از عدسی 1 محاسبه کنید

اولین قسمت محاسبه بزرگنمایی چند لنز همان محاسبه بزرگنمایی یک لنز است. با نزدیکترین عدسی به جسم شروع کنید ، از معادله عدسی برای پیدا کردن فاصله از تصویر تشکیل شده استفاده کنید ، سپس از معادله بزرگنمایی برای پیدا کردن ارتفاع و بزرگنمایی تصویر استفاده کنید. برای مشاهده بیشتر محاسبات بزرگنمایی تک لنز اینجا را کلیک کنید.

• از محاسبات ما در روش 1 بالا ، متوجه می شویم که اولین لنز تصویری به ارتفاع تولید می کند - 3 ، 996 سانتی متر ، فاصله 33.3 سانتی متر پشت لنز ، و در بزرگنمایی - 0, 666.

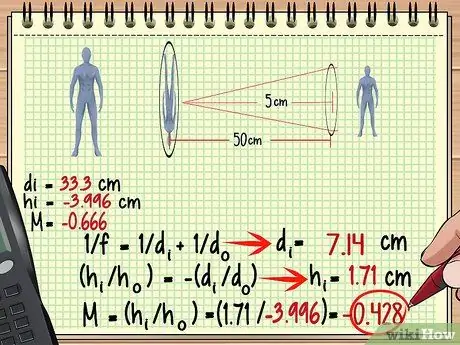
مرحله 3. از تصویر لنز اول به عنوان شیء لنز دوم استفاده کنید

در حال حاضر ، یافتن بزرگنمایی ، ارتفاع و بیشتر برای لنز دوم بسیار آسان است - فقط از همان روشی که برای لنز اول استفاده کرده اید استفاده کنید ، فقط این بار با تصویر به عنوان یک شی برخورد کنید. به یاد داشته باشید که فاصله تصویر تا لنز دوم همیشه با فاصله جسم تا لنز اول یکسان نیست.

• در مثال بالا ، از آنجا که تصویر 33.3 سانتی متر پشت اولین لنز تشکیل شده است ، فاصله 50-33.3 = است 16.7 سانتی متر مقابل لنز دوم بیایید از این اندازه گیری و فاصله کانونی لنز دوم برای یافتن تصویری که از لنز دوم تشکیل شده است استفاده کنیم.

  1/f = 1/d_o + 1/روز_من

  1/5 = 1/16 ، 7 + 1/روز_من

  0 ، 2 - 0 ، 0599 = 1/روز_من

  0 ، 14 = 1/روز_من

  د_من = 7 ، 14 سانتی متر

• حالا می توانیم h را محاسبه کنیم_من و M برای لنز دوم:

  (ساعت_من/ساعت_o) = -(د_من/د_o)

  (ساعت_من/-3, 996) = -(7, 14/16, 7)

  ساعت_من = -(0 ، 427) x -3 ، 996

  ساعت_من = 1 ، 71 سانتی متر

  M = (ساعت_من/ساعت_o)

  M = (1 ، 71/-3 ، 996) = - 0, 428

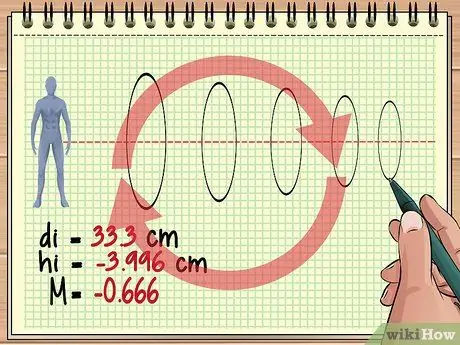
مرحله 4. محاسبه اینگونه را برای لنزهای اضافی ادامه دهید

اگر سه ، چهار یا صدها عدسی در جلوی یک شی قرار گرفته باشند ، این رویکرد اصلی یکسان است. برای هر لنز ، تصویر لنز قبلی را به عنوان جسم در نظر بگیرید و از معادله لنز و معادله بزرگنمایی برای یافتن پاسخ مورد نظر خود استفاده کنید.

به خاطر داشته باشید که هر لنز بعدی می تواند به طور مداوم تصویر تشکیل شده را وارونه کند. به عنوان مثال ، مقدار بزرگنمایی که قبلاً به دست آوردیم (-0 ، 428) نشان می دهد که تصویری که قرار است ببینیم تقریباً 4/10 اندازه اندازه واقعی شیء است ، اما عمود است ، زیرا تصویر لنز قبلی معکوس است

نکات

• دوربین های دوچشمی معمولاً توضیحاتی در مورد مشخصات بزرگنمایی به صورت چند برابر یک عدد دیگر ارائه می دهند. به عنوان مثال ، دوربین های دو چشمی را می توان 8x25 یا 8x40 مشخص کرد. وقتی چنین نوشته می شود ، اولین عدد بزرگنمایی دوربین دو چشمی است. مهم نیست حتی اگر در مثال ذکر شده ، این دو عدد از نظر اندازه متفاوت باشند ، هر دو دوربین دو چشمی دارای بزرگنمایی 8 برابر هستند. عدد دوم نشان می دهد که چگونه تصویر با دوربین دوچشمی روشن می شود.
• به یاد داشته باشید که برای لوپ تک لنز ، اگر فاصله جسم بیشتر از فاصله کانونی لنز باشد ، بزرگنمایی منفی خواهد بود. این بدان معنا نیست که تصویر تشکیل شده کوچکتر خواهد بود. در این حالت ، بزرگنمایی همچنان رخ می دهد ، اما تصویر تشکیل شده توسط ناظر به صورت وارونه (از بالا به پایین) مشاهده می شود.